Planar Straight Line Drawing of K4

Graph that can be embedded in the aeroplane

Instance graphs
Planar	Nonplanar
Butterfly graph	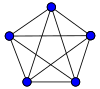Complete graph Thou 5
Complete graph K 4	Utility graph One thousand iii,three

In graph theory, a planar graph is a graph that can be embedded in the airplane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be fatigued in such a way that no edges cross each other.^{[1] [two]} Such a drawing is chosen a aeroplane graph or planar embedding of the graph. A plane graph tin be defined as a planar graph with a mapping from every node to a signal on a plane, and from every border to a plane curve on that aeroplane, such that the extreme points of each curve are the points mapped from its terminate nodes, and all curves are disjoint except on their extreme points.

Every graph that can be drawn on a aeroplane tin can be fatigued on the sphere as well, and vice versa, by means of stereographic projection.

Plane graphs can be encoded by combinatorial maps or rotation systems.

An equivalence class of topologically equivalent drawings on the sphere, usually with additional assumptions such as the absence of isthmuses, is called a planar map. Although a aeroplane graph has an external or unbounded face, none of the faces of a planar map has a particular status.

Planar graphs generalize to graphs drawable on a surface of a given genus. In this terminology, planar graphs have genus 0, since the plane (and the sphere) are surfaces of genus 0. Meet "graph embedding" for other related topics.

Planarity criteria [edit]

Kuratowski's and Wagner'due south theorems [edit]

The Polish mathematician Kazimierz Kuratowski provided a characterization of planar graphs in terms of forbidden graphs, at present known as Kuratowski's theorem:

A finite graph is planar if and merely if information technology does non incorporate a subgraph that is a subdivision of the complete graph Thou ₅ or the complete bipartite graph ${\displaystyle K_{3,3}}$ (utility graph).

A subdivision of a graph results from inserting vertices into edges (for example, irresolute an edge •——• to •—•—•) naught or more times.

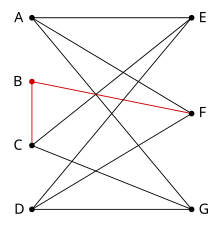
An instance of a graph with no Yard ₅ or Thou _3,3 subgraph. Yet, it contains a subdivision of K _3,3 and is therefore non-planar.

Instead of considering subdivisions, Wagner'south theorem deals with minors:

A finite graph is planar if and only if it does not have ${\displaystyle K_{5}}$ or ${\displaystyle K_{3,3}}$ as a minor.

A small of a graph results from taking a subgraph and repeatedly contracting an edge into a vertex, with each neighbor of the original end-vertices becoming a neighbor of the new vertex.

An blitheness showing that the Petersen graph contains a minor isomorphic to the K_three,3 graph, and is therefore not-planar

Klaus Wagner asked more generally whether whatsoever small-scale-closed class of graphs is determined by a finite set of "forbidden minors". This is now the Robertson–Seymour theorem, proved in a long serial of papers. In the language of this theorem, ${\displaystyle K_{5}}$ and ${\displaystyle K_{3,3}}$ are the forbidden minors for the class of finite planar graphs.

Other criteria [edit]

In practise, it is difficult to use Kuratowski'due south criterion to quickly decide whether a given graph is planar. Withal, there exist fast algorithms for this problem: for a graph with n vertices, it is possible to determine in fourth dimension O(n) (linear time) whether the graph may be planar or not (see planarity testing).

For a unproblematic, continued, planar graph with v vertices and due east edges and f faces, the following simple conditions hold for v ≥ 3:

• Theorem 1. due east ≤ threefive − 6;
• Theorem 2. If there are no cycles of length 3, then e ≤ iiv − iv.
• Theorem 3. f ≤ 2v − 4.

In this sense, planar graphs are sparse graphs, in that they have only O(v) edges, asymptotically smaller than the maximum O(five ²). The graph K _iii,3, for case, has half-dozen vertices, 9 edges, and no cycles of length three. Therefore, by Theorem 2, information technology cannot be planar. These theorems provide necessary conditions for planarity that are not sufficient conditions, and therefore can only be used to show a graph is not planar, not that information technology is planar. If both theorem one and 2 neglect, other methods may be used.

• Whitney'south planarity criterion gives a characterization based on the existence of an algebraic dual;
• Mac Lane's planarity benchmark gives an algebraic characterization of finite planar graphs, via their bike spaces;
• The Fraysseix–Rosenstiehl planarity criterion gives a characterization based on the beingness of a bipartition of the cotree edges of a depth-first search tree. It is central to the left-correct planarity testing algorithm;
• Schnyder'southward theorem gives a characterization of planarity in terms of partial social club dimension;
• Colin de Verdière'due south planarity criterion gives a characterization based on the maximum multiplicity of the second eigenvalue of certain Schrödinger operators divers by the graph.
• The Hanani–Tutte theorem states that a graph is planar if and only if information technology has a cartoon in which each independent pair of edges crosses an even number of times; it can be used to characterize the planar graphs via a system of equations modulo 2.

Properties [edit]

Euler's formula [edit]

Euler'south formula states that if a finite, continued, planar graph is fatigued in the plane without any edge intersections, and 5 is the number of vertices, e is the number of edges and f is the number of faces (regions divisional by edges, including the outer, infinitely large region), then

${\displaystyle v-e+f=two.}$

As an illustration, in the butterfly graph given higher up, v = v, eastward = 6 and f = 3. In full general, if the property holds for all planar graphs of f faces, any change to the graph that creates an additional face while keeping the graph planar would keep 5 −e +f an invariant. Since the property holds for all graphs with f = 2, by mathematical induction it holds for all cases. Euler'south formula can also be proved as follows: if the graph isn't a tree, then remove an edge which completes a wheel. This lowers both e and f by ane, leaving five − e +f constant. Repeat until the remaining graph is a tree; copse have v =eastward + 1 and f = 1, yielding v −e +f = 2, i. due east., the Euler feature is 2.

In a finite, connected, simple, planar graph, any face (except possibly the outer one) is bounded by at least three edges and every border touches at most ii faces; using Euler'southward formula, one tin then show that these graphs are thin in the sense that if v ≥ iii:

${\displaystyle east\leq 3v-6.}$

Euler's formula is also valid for convex polyhedra. This is no coincidence: every convex polyhedron can be turned into a continued, simple, planar graph by using the Schlegel diagram of the polyhedron, a perspective projection of the polyhedron onto a airplane with the center of perspective called nearly the center of one of the polyhedron'due south faces. Not every planar graph corresponds to a convex polyhedron in this mode: the copse do not, for example. Steinitz'due south theorem says that the polyhedral graphs formed from convex polyhedra are precisely the finite 3-connected uncomplicated planar graphs. More generally, Euler'south formula applies to any polyhedron whose faces are simple polygons that form a surface topologically equivalent to a sphere, regardless of its convexity.

Average degree [edit]

Connected planar graphs with more than one edge obey the inequality ${\displaystyle 2e\geq 3f}$ , because each confront has at to the lowest degree three face up-edge incidences and each edge contributes exactly two incidences. Information technology follows via algebraic transformations of this inequality with Euler'southward formula ${\displaystyle v-e+f=ii}$ that for finite planar graphs the average degree is strictly less than six. Graphs with higher average degree cannot be planar.

Coin graphs [edit]

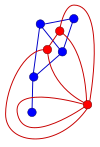
Instance of the circle packing theorem on K⁻ ₅, the complete graph on five vertices, minus 1 edge.

We say that 2 circles drawn in a plane osculation (or osculate) whenever they intersect in exactly one point. A "coin graph" is a graph formed past a gear up of circles, no two of which take overlapping interiors, by making a vertex for each circle and an edge for each pair of circles that kiss. The circumvolve packing theorem, commencement proved past Paul Koebe in 1936, states that a graph is planar if and but if it is a coin graph.

This result provides an easy proof of Fáry's theorem, that every simple planar graph can exist embedded in the airplane in such a way that its edges are straight line segments that do not cross each other. If one places each vertex of the graph at the middle of the respective circumvolve in a coin graph representation, then the line segments between centers of kissing circles practice not cross any of the other edges.

Planar graph density [edit]

The meshedness coefficient or density ${\displaystyle D}$ of a planar graph, or network, is the ratio of the number ${\displaystyle f-one}$ of bounded faces (the same as the circuit rank of the graph, by Mac Lane's planarity criterion) by its maximal possible values ${\displaystyle 2v-5}$ for a graph with ${\displaystyle v}$ vertices:

${\displaystyle D={\frac {f-one}{2v-v}}}$

The density obeys ${\displaystyle 0\leq D\leq i}$ , with ${\displaystyle D=0}$ for a completely sparse planar graph (a tree), and ${\displaystyle D=1}$ for a completely dense (maximal) planar graph.^[three]

Dual graph [edit]

A planar graph and its dual

Given an embedding G of a (not necessarily elementary) continued graph in the aeroplane without edge intersections, we construct the dual graph G* every bit follows: we choose one vertex in each face of 1000 (including the outer face) and for each edge eastward in G we introduce a new edge in G* connecting the two vertices in G* corresponding to the two faces in Thousand that meet at e. Furthermore, this border is fatigued so that information technology crosses e exactly once and that no other border of Thou or G* is intersected. And then Grand* is once more the embedding of a (not necessarily unproblematic) planar graph; it has every bit many edges as G, equally many vertices equally G has faces and every bit many faces as M has vertices. The term "dual" is justified past the fact that Thousand** = One thousand; hither the equality is the equivalence of embeddings on the sphere. If Thousand is the planar graph corresponding to a convex polyhedron, and then G* is the planar graph respective to the dual polyhedron.

Duals are useful because many backdrop of the dual graph are related in simple ways to backdrop of the original graph, enabling results to be proven about graphs by examining their dual graphs.

While the dual synthetic for a particular embedding is unique (up to isomorphism), graphs may have dissimilar (i.e. non-isomorphic) duals, obtained from dissimilar (i.eastward. non-homeomorphic) embeddings.

Families of planar graphs [edit]

Maximal planar graphs [edit]

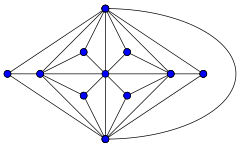
A simple graph is called maximal planar if it is planar merely calculation any edge (on the given vertex set) would destroy that belongings. All faces (including the outer ane) are then bounded by iii edges, explaining the alternative term aeroplane triangulation. The culling names "triangular graph"^[4] or "triangulated graph"^[5] have also been used, but are cryptic, as they more than commonly refer to the line graph of a complete graph and to the chordal graphs respectively. Every maximal planar graph is a least 3-connected.

If a maximal planar graph has v vertices with v > 2, and then it has precisely 3v − half dozen edges and 2v − iv faces.

Apollonian networks are the maximal planar graphs formed by repeatedly splitting triangular faces into triples of smaller triangles. Equivalently, they are the planar 3-copse.

Strangulated graphs are the graphs in which every peripheral cycle is a triangle. In a maximal planar graph (or more mostly a polyhedral graph) the peripheral cycles are the faces, so maximal planar graphs are strangulated. The strangulated graphs include also the chordal graphs, and are exactly the graphs that can exist formed by clique-sums (without deleting edges) of complete graphs and maximal planar graphs.^[six]

Outerplanar graphs [edit]

Outerplanar graphs are graphs with an embedding in the plane such that all vertices belong to the unbounded face up of the embedding. Every outerplanar graph is planar, but the converse is not true: K ₄ is planar simply non outerplanar. A theorem like to Kuratowski'southward states that a finite graph is outerplanar if and only if it does not incorporate a subdivision of Grand ₄ or of M _2,3. The above is a directly corollary of the fact that a graph G is outerplanar if the graph formed from Chiliad by adding a new vertex, with edges connecting it to all the other vertices, is a planar graph.^[vii]

A 1-outerplanar embedding of a graph is the same every bit an outerplanar embedding. For k > 1 a planar embedding is k-outerplanar if removing the vertices on the outer confront results in a (k − 1)-outerplanar embedding. A graph is m-outerplanar if it has a k-outerplanar embedding.

Halin graphs [edit]

A Halin graph is a graph formed from an undirected plane tree (with no caste-two nodes) by connecting its leaves into a cycle, in the order given past the plane embedding of the tree. Equivalently, it is a polyhedral graph in which one face is adjacent to all the others. Every Halin graph is planar. Similar outerplanar graphs, Halin graphs take low treewidth, making many algorithmic problems on them more easily solved than in unrestricted planar graphs.^[8]

Upward planar graphs [edit]

An upward planar graph is a directed acyclic graph that tin be drawn in the aeroplane with its edges equally non-crossing curves that are consistently oriented in an upward direction. Non every planar directed acyclic graph is upwardly planar, and it is NP-complete to test whether a given graph is upward planar.

Convex planar graphs [edit]

A planar graph is said to exist convex if all of its faces (including the outer face) are convex polygons. Non all planar graphs have a convex embedding (e.one thousand. the complete bipartite graph ${\displaystyle K_{2,4}}$ ). A sufficient condition that a graph tin can be drawn convexly is that information technology is a subdivision of a 3-vertex-continued planar graph. Tutte's spring theorem even states that for elementary iii-vertex-connected planar graphs the position of the inner vertices can be chosen to be the average of its neighbors.

Word-representable planar graphs [edit]

Word-representable planar graphs include triangle-free planar graphs and, more by and large, 3-colourable planar graphs,^[9] as well as certain face up subdivisions of triangular grid graphs,^[10] and certain triangulations of grid-covered cylinder graphs.^[eleven]

Theorems [edit]

Enumeration of planar graphs [edit]

The asymptotic for the number of (labeled) planar graphs on ${\displaystyle n}$ vertices is ${\displaystyle g\cdot north^{-seven/2}\cdot \gamma ^{north}\cdot north!}$ , where ${\displaystyle \gamma \approx 27.22687}$ and ${\displaystyle g\approx 0.43\times 10^{-5}}$ .^[12]

Near all planar graphs accept an exponential number of automorphisms.^[thirteen]

The number of unlabeled (non-isomorphic) planar graphs on ${\displaystyle n}$ vertices is between ${\displaystyle 27.ii^{n}}$ and ${\displaystyle 30.06^{northward}}$ .^[14]

Other results [edit]

The 4 colour theorem states that every planar graph is 4-colorable (i.east., 4-partite).

Fáry'southward theorem states that every uncomplicated planar graph admits a representation as a planar direct-line graph. A universal point ready is a fix of points such that every planar graph with n vertices has such an embedding with all vertices in the point set; there be universal point sets of quadratic size, formed by taking a rectangular subset of the integer lattice. Every elementary outerplanar graph admits an embedding in the plane such that all vertices lie on a stock-still circle and all edges are straight line segments that lie inside the disk and don't intersect, and then due north-vertex regular polygons are universal for outerplanar graphs.

Scheinerman'due south theorize (at present a theorem) states that every planar graph tin can exist represented every bit an intersection graph of line segments in the aeroplane.

The planar separator theorem states that every n-vertex planar graph tin can exist partitioned into two subgraphs of size at near 2n/3 by the removal of O(√ n ) vertices. As a consequence, planar graphs besides accept treewidth and branch-width O(√ n ).

The planar product structure theorem states that every planar graph is a subgraph of the stiff graph product of a graph of treewidth at most 8 and a path.^[fifteen] This effect has been used to prove that planar graphs have bounded queue number, bounded non-repetitive chromatic number, and universal graphs of nearly-linear size. It also has applications to vertex ranking^[16] and p-centered colouring^[17] of planar graphs.

For two planar graphs with five vertices, information technology is possible to determine in time O(v) whether they are isomorphic or non (see too graph isomorphism trouble).^[18]

Generalizations [edit]

An apex graph is a graph that may be fabricated planar by the removal of 1 vertex, and a k-apex graph is a graph that may be fabricated planar by the removal of at nearly 1000 vertices.

A 1-planar graph is a graph that may exist drawn in the plane with at most 1 unproblematic crossing per edge, and a one thousand-planar graph is a graph that may be fatigued with at most yard elementary crossings per border.

A map graph is a graph formed from a set of finitely many simply-continued interior-disjoint regions in the aeroplane by connecting two regions when they share at least i boundary point. When at most 3 regions meet at a point, the result is a planar graph, but when iv or more regions meet at a point, the effect can be nonplanar.

A toroidal graph is a graph that can exist embedded without crossings on the torus. More generally, the genus of a graph is the minimum genus of a two-dimensional surface into which the graph may be embedded; planar graphs take genus nothing and nonplanar toroidal graphs have genus one.

Whatever graph may be embedded into three-dimensional space without crossings. All the same, a 3-dimensional analogue of the planar graphs is provided by the linklessly embeddable graphs, graphs that can exist embedded into three-dimensional space in such a way that no two cycles are topologically linked with each other. In illustration to Kuratowski's and Wagner's characterizations of the planar graphs equally beingness the graphs that do not contain K _five or K _3,iii as a minor, the linklessly embeddable graphs may be characterized every bit the graphs that practice non incorporate as a pocket-size whatever of the vii graphs in the Petersen family. In analogy to the characterizations of the outerplanar and planar graphs as existence the graphs with Colin de Verdière graph invariant at about ii or 3, the linklessly embeddable graphs are the graphs that take Colin de Verdière invariant at virtually four.

Come across also [edit]

• Combinatorial map a combinatorial object that tin encode plane graphs
• Planarization, a planar graph formed from a drawing with crossings by replacing each crossing signal by a new vertex
• Thickness (graph theory), the smallest number of planar graphs into which the edges of a given graph may exist partitioned
• Planarity, a puzzle reckoner game in which the objective is to embed a planar graph onto a airplane
• Sprouts (game), a pencil-and-paper game where a planar graph subject to certain constraints is constructed equally part of the game play
• 3 utilities problem, a popular puzzle

Notes [edit]

1. ^ Trudeau, Richard J. (1993). Introduction to Graph Theory (Corrected, enlarged republication. ed.). New York: Dover Pub. p. 64. ISBN978-0-486-67870-2 . Retrieved 8 Baronial 2012. Thus a planar graph, when drawn on a apartment surface, either has no edge-crossings or can be redrawn without them.
2. ^ Barthelemy, M. (2017). Morphogenesis of Spatial Networks. New York: Springer. p. six.
3. ^ Buhl, J.; Gautrais, J.; Sole, R.V.; Kuntz, P.; Valverde, S.; Deneubourg, J.L.; Theraulaz, 1000. (2004), "Efficiency and robustness in ant networks of galleries", European Physical Journal B, Springer-Verlag, 42 (one): 123–129, Bibcode:2004EPJB...42..123B, doi:x.1140/epjb/e2004-00364-9, S2CID 14975826 .
4. ^ Schnyder, W. (1989), "Planar graphs and poset dimension", Order, 5 (4): 323–343, doi:10.1007/BF00353652, MR 1010382, S2CID 122785359 .
5. ^ Bhasker, Jayaram; Sahni, Sartaj (1988), "A linear algorithm to find a rectangular dual of a planar triangulated graph", Algorithmica, 3 (one–4): 247–278, doi:10.1007/BF01762117, S2CID 2709057 .
6. ^ Seymour, P. D.; Weaver, R. W. (1984), "A generalization of chordal graphs", Journal of Graph Theory, viii (2): 241–251, doi:10.1002/jgt.3190080206, MR 0742878 .
7. ^ Felsner, Stefan (2004), "1.4 Outerplanar Graphs and Convex Geometric Graphs", Geometric graphs and arrangements, Advanced Lectures in Mathematics, Friedr. Vieweg & Sohn, Wiesbaden, pp. 6–seven, doi:x.1007/978-3-322-80303-0_1, ISBNthree-528-06972-4, MR 2061507
8. ^ Sysło, Maciej M.; Proskurowski, Andrzej (1983), "On Halin graphs", Graph Theory: Proceedings of a Conference held in Lagów, Poland, February 10–thirteen, 1981, Lecture Notes in Mathematics, vol. 1018, Springer-Verlag, pp. 248–256, doi:10.1007/BFb0071635 .
9. ^ "1000. Halldórsson, S. Kitaev and A. Pyatkin. Semi-transitive orientations and word-representable graphs, Discr. Appl. Math. 201 (2016), 164-171".
10. ^ T. Z. Q. Chen, S. Kitaev, and B. Y. Lord's day. Word-representability of face subdivisions of triangular grid graphs, Graphs and Combin. 32(5) (2016), 1749-1761.
11. ^ T. Z. Q. Chen, S. Kitaev, and B. Y. Sunday. Word-representability of triangulations of filigree-covered cylinder graphs, Discr. Appl. Math. 213 (2016), lx-70.
12. ^ Giménez, Omer; Noy, Marc (2009). "Asymptotic enumeration and limit laws of planar graphs". Periodical of the American Mathematical Club. 22 (two): 309–329. arXiv:math/0501269. Bibcode:2009JAMS...22..309G. doi:x.1090/s0894-0347-08-00624-three. S2CID 3353537.
13. ^ McDiarmid, Colin; Steger, Angelika; Welsh, Dominic J.A. (2005). "Random planar graphs". Journal of Combinatorial Theory, Serial B. 93 (ii): 187–205. CiteSeerXx.one.ane.572.857. doi:10.1016/j.jctb.2004.09.007.
14. ^ Bonichon, North.; Gavoille, C.; Hanusse, Northward.; Poulalhon, D.; Schaeffer, 1000. (2006). "Planar Graphs, via Well-Orderly Maps and Copse". Graphs and Combinatorics. 22 (2): 185–202. CiteSeerX10.1.1.106.7456. doi:x.1007/s00373-006-0647-two. S2CID 22639942.
15. ^ Dujmović, Vida; Joret, Gwenäel; Micek, Piotr; Morin, Pat; Ueckerdt, Torsten; Wood, David R. (2020), "Planar graphs accept divisional queue number", Journal of the ACM, 67 (4): 22:i–22:38, arXiv:1904.04791, doi:10.1145/3385731
16. ^ Bose, Prosenjit; Dujmović, Vida; Javarsineh, Mehrnoosh; Morin, Pat (2020), Asymptotically optimal vertex ranking of planar graphs, arXiv:2007.06455
17. ^ Dębski, Michał; Felsner, Stefan; Micek, Piotr; Schröder, Felix (2019), Improved bounds for centered colorings, arXiv:1907.04586
18. ^ I. South. Filotti, Jack N. Mayer. A polynomial-time algorithm for determining the isomorphism of graphs of fixed genus. Proceedings of the twelfth Annual ACM Symposium on Theory of Calculating, p.236–243. 1980.

References [edit]

• Kuratowski, Kazimierz (1930), "Sur le problème des courbes gauches en topologie" (PDF), Fundamenta Mathematicae (in French), 15: 271–283, doi:10.4064/fm-xv-i-271-283 .
• Wagner, G. (1937), "Über eine Eigenschaft der ebenen Komplexe", Mathematische Annalen (in German), 114: 570–590, doi:10.1007/BF01594196, S2CID 123534907 .
• Boyer, John Yard.; Myrvold, Wendy J. (2005), "On the cutting edge: Simplified O(due north) planarity by edge addition" (PDF), Journal of Graph Algorithms and Applications, viii (3): 241–273, doi:ten.7155/jgaa.00091 .
• McKay, Brendan; Brinkmann, Gunnar, A useful planar graph generator .
• de Fraysseix, H.; Ossona de Mendez, P.; Rosenstiehl, P. (2006), "Trémaux trees and planarity", International Journal of Foundations of Computer Science, 17 (v): 1017–1029, arXiv:math/0610935, doi:10.1142/S0129054106004248, S2CID 40107560 . Special Result on Graph Cartoon.
• D.A. Bader and S. Sreshta, A New Parallel Algorithm for Planarity Testing, UNM-ECE Technical Study 03-002, Oct 1, 2003.
• Fisk, Steve (1978), "A brusk proof of Chvátal'south watchman theorem", Journal of Combinatorial Theory, Series B, 24 (three): 374, doi:ten.1016/0095-8956(78)90059-X .

External links [edit]

• Edge Add-on Planarity Algorithm Source Code, version 1.0 — Free C source code for reference implementation of Boyer–Myrvold planarity algorithm, which provides both a combinatorial planar embedder and Kuratowski subgraph isolator. An open source project with gratuitous licensing provides the Edge Addition Planarity Algorithms, current version.
• Public Implementation of a Graph Algorithm Library and Editor — GPL graph algorithm library including planarity testing, planarity embedder and Kuratowski subgraph exhibition in linear time.
• Boost Graph Library tools for planar graphs, including linear time planarity testing, embedding, Kuratowski subgraph isolation, and direct-line cartoon.
• 3 Utilities Puzzle and Planar Graphs
• NetLogo Planarity model — NetLogo version of John Tantalo'due south game

frostwishis.blogspot.com

Source: https://en.wikipedia.org/wiki/Planar_graph

Share this post